White Dwarf Stars
Brilliant star – Image by David Zydd from Pixabay
The age of white dwarf stars is one of the best ways to help determine the age of the universe. We took a brief look at how this is done.
But to really understand how this is done, it is necessary to take a deep dive into what a white dwarf star really is, how they form, how they cool off, how all white dwarfs are nearly identical, and how they are able to determine the age of the universe.
White dwarf stars are the dead remnants of old stars that are no longer burning nuclear fuel; they are still hot, radiating heat into space and slowly cooling down. More than 98 percent of all stars will end up as white dwarfs at the end of their lives; in the distant future, our sun will share in that fate. A white dwarf will be very common in the cold, distant future of the universe, but it is also one of the most interesting objects in the sky because it is not made out of ordinary matter but of something called “degenerate matter.”
Low Mass Stars
Stars that are about half the mass of the sun will never end up as a white dwarf; they will never complete the full set of proton-proton reactions that keep a star burning.
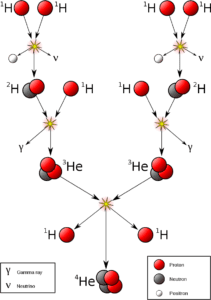
Proton-Proton Reaction
The first step involves a proton combining with another proton. Since both of these protons contain a positive change, the temperature at the center of a star has to be incredibly hot for this combination to occur. Since they are of the same charge, they tend to repel each other, especially at very close distances. Because of this electrostatic repulsion, most of these close interactions will quickly fall apart. Rarely, however, the two protons will get close enough so that the strong nuclear force will bring them together.
The second step involves the weak nuclear force where a quark in one of the protons changes so that the proton becomes a neutron, and the proton-proton pair becomes a proton-neutron pair or deuterium. When the proton becomes a neutron, a positron and an electron neutrino are released. Positrons quickly interact with an electron mutually destroying each other producing two gamma rays.
The third step involves the fusion of a deuterium nucleus with another proton forming a helium nucleus with two protons and one neutron.
The fourth step is whereby two helium nuclei fuse to form two helium nuclei with two protons and two neutrons, along with two protons.
These four steps have the effect of taking two hydrogen atoms and fusing them into helium atoms. The mass of the helium atom is less than the combined mass of the two helium atoms; this difference is the mass that is converted into energy which makes the sun radiate energy and shine.
Stars with less than half the mass of the sun are not hot enough for the fourth step to occur. Because of this inability to complete the conversion of hydrogen into helium, lower mass stars will shine much longer than the sun – may be even ten times longer or more.
Red Subgiant Stars
Stars that have at least half the mass of the sun will successfully convert more and more of their hydrogen fuel into helium and over billions of years, will finally exhaust their energy supply. The supply of hydrogen available for nuclear reactions is only that which is found in the core of the star, representing only about ten percent of its total volume.
Eventually, the core runs out of hydrogen and it cools down; gravity will squeeze the star causing it to heat up. The core of the star heats up due to gravitational contraction and this heat causes the rest of the star outside of the core to expand. The outer layers of the star expand and produce a larger surface area and radiate away energy from the star over a larger surface area causing the surface of the star to cool. This unusual situation is that the center of a red subgiant and giant star is extremely hot, while the surface of the star is cooling down.
The star becomes brighter (more luminous) because it has a greater surface area, but cooler because the larger surface area radiates heat away from the star more quickly.
Red Giant Stars
Mira – a red giant star seen through the Hubble telescope to be irregular in size.
Eventually, the core heats up enough to produce a high enough temperature to ignite the hydrogen around it producing a burst of energy. The additional heat produced from the ignition of a hydrogen shell around the core causes the star to expand further causing the surface area to increase, radiate heat off more effectively, and become cooler.
The star now becomes a “red giant” as its size increases outward and the surface temperature cools further.
Electron Degeneracy in White Dwarf Stars
The core of an intermediate-mass star like our sun will undergo a strange transformation when it becomes a red giant star. The inner core of the star consists of inert helium that cannot undergo nuclear synthesis to large elements as the temperature is just too low. This means that the effect of gravity will crush the core into a smaller and smaller size until it cannot be compressed any further. The reason matter cannot be infinitely compressed has to do with the electrons orbiting the nucleus.
Electrons can only inhabit certain energy states in their travel around the nucleus, and there are only a certain number of electrons that can occupy a given energy level. Furthermore, the electrons that do occupy the same energy level cannot be identical; they cannot have the same exact properties of energy, spin, and motion.
This all means that there are only a certain number of electrons that are able to be accommodated in orbits around the nucleus. A given electron cannot occupy energy levels (or orbits) that are occupied by another electron. This is something that is called the “Pauli Exclusion Principle” and is one of the well-known properties of subatomic particles. In fact, this principle relates to the stability of ordinary matter – why matter takes up space. Consider if there were no limitations to the number of electrons that could occupy the lowest energy levels in their journey around the nucleus of an atom. In this case, all matter would collapse and lose a significant portion of its volume.
The core of our red giant star now has electrons that are compressed into the lowest volume possible around their respective nuclei – every energy state is occupied; they cannot be compressed any further due to the Paul Exclusion Principle. This means that the force pushing back against gravitational compression is no longer heat – but rather electron degeneracy.
Furthermore, the sea of electrons surrounding the helium nuclei in the core will immediately smooth out any temperature differences in the core; the core becomes isothermal in that it has the same temperature throughout its volume.
The star is not totally out of tricks once it has used up much of the hydrogen at its core. If it is big enough, and if enough temperature can be generated, it can get a new lease on life by starting to burn helium.
Carbon-Oxygen Core: The Triple Alpha Process
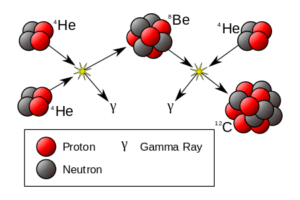
Triple Alpha Process
When the temperature of the core reaches about 100 million degrees K, helium nuclei in the center core have enough energy and are moving quickly enough for them to start colliding with each other. Remember the helium nucleus has two protons and two neutrons so it has a double positive charge. For two double-positive charged nuclei to fuse with each other requires tremendous energy due to the electrostatic repulsion of the positive charge nuclei.
When two helium ions fuse they form a beryllium nucleus. Some of the mass of the two helium nuclei is converted into gamma radiation when this fusion occurs. The beryllium nucleus with four protons and four neutrons is very unstable and very quickly falls apart into two helium nuclei again.
Very occasionally, three helium nuclei will all strike each other at virtually the same instant; in this case, the three helium nuclei will form a carbon atom with six protons and six neutrons which is stable. A helium nucleus is also historically known as an alpha particle, and the process of three helium nuclei simultaneously forming a carbon nucleus is called the “triple-alpha process.” Oxygen is produced when a carbon atom collides with another helium atom to produce the oxygen nucleus eight protons and eight neutrons.
Over time, using the triple-alpha process, the core of a star is gradually changed from helium to carbon and oxygen. When a star finally dies in an explosion producing a planetary nebula (will discuss more below), some of this carbon and oxygen in the star will be expelled into space. Ultimately, all of the carbon and oxygen on our planet (whether carbon in the form of graphite, coal, or diamond or combined with oxygen and hydrogen to form hydrocarbons and organic molecules) was made in the core of the red giant stars.
In other words, all the oxygen in the air we all breathe every day originated in the remote past from the fiery furnace in the core of a long-dead star.
The aging star now resembles an onion with a very dense core made of carbon and oxygen of degenerate matter, a layer around the core composed of helium being fused to carbon in the triple-alpha process, and another layer of hydrogen to helium fusion, and then finally the rest of the star composed of inert hydrogen. As the age of the star further, heat in the center of the star continues to rise, causing expansion of the outer inert hydrogen layer producing a larger even more luminous star.
Red Star Instability
Planetary Nebula
A star is very stable during most of its existence. There are variable stars that periodically increase in luminosity but generally, this variability is controlled, orderly, and predictable. Stars who reach the red giant phase of their existence grow more unstable. Giant stars experience cooling in their outermost layers due to their huge size which spreads out their heat production over a larger area. Sometimes, the cooling allows electrons to pair with their nuclei producing stable atoms allowing more of its heat energy to escape.
Heat energy then leaves the outermost layers of the stay producing cooling; this makes the gas denser and it falls back into the star. The collapsing outer layers of the star slam against the hot interior causing these layers to then expand toward the surface. The star then expands and contracts with outer layers collapsing in toward the star center. Sometimes the expansion of the heated outer layers results in their escaping the gravitational attraction of the star. This causes these layers to puff out into space. This gas layer then is heated up by the star producing a luminous planetary nebula. This sloughing of the outer layers of the star continues until all that is left behind is the extremely hot, small central core of the red giant – about ten percent of the volume of the original star.
Gas from the red giant stars can expel rings of gas at speeds of up to thousands of kilometers per second, with a loss of about 0.001% of the star’s mass per year. At this rate, the star loses everything outside its central core in about 100,000 years.
The remaining cores of the stars have temperatures of about 150,000 K and are white-hot. They emit most of their heat in the ultraviolet spectrum meaning they are very dim in regular visible light.
White Dwarfs
The white dwarf stars have a small surface area being about the same size as the Earth, with small luminosities. Even though they are common throughout the universe, they are quite small with dim luminosities and are difficult to identify.
In 1862, telescope maker Alvin Clark was testing out his new 18.5-inch refracting telescope on the brightest star in the sky, Sirius with a magnitude brightness of -1.46. While doing so, he managed to view its dim companion star Sirius B with a magnitude brightness of 8 or 377 times dimmer than its brilliant companion star. They did not realize it at the time, but they had just found the nearest white dwarf star.
Since Sirius and its companion star are both approximately the same distance from the earth (2.64 parsecs), their difference in brightness must be because they are either different temperatures, different sizes, or both.
In order to better characterize the white dwarf companion of Sirius, it is necessary to take an excursion into determining the temperature and the size of stars.
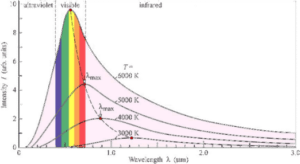
Black Body Spectrum
Measuring a Star’s Temperature. Stars shine in a manner approximating a black body radiator. Black body radiators are said to be in thermal equilibrium with their environment whose emission light spectrum depends only upon its temperature. When you heat up your stove element, for example, it assumes a red color when it reaches its heated state; this color is the dominant color emitted by the stove element. However, the element also emits some radiation at all other wavelengths although at much less power. The light wavelength with the most power can give the surface temperature of the star.
If there are two stars of the same temperature but one is brighter than the other, the brighter star has to have a higher surface area. Put another way, the luminosity of a star – the total energy released per second – depends both on its surface area and temperature.
This relationship has become formalized in the Stefan-Boltzmann law. This law states that is an object gets bigger and has a larger surface area, the luminosity increases proportionately; if you double the surface area you will double the luminosity. However, as the temperature increases, the luminosity for up much more dramatically by the fourth power. So, if you double the surface temperature, you will increase the luminosity by 16 times.
Using these relationships, it is possible to calculate the diameter of the white dwarf star binary of Sirius; its dominant color provides its temperate; since we know the distance to the star and its brightness, we can calculate its luminosity. Once we know the luminosity (about four times hotter or sixteen times more luminous than the Sun), we can calculate the diameter of the star which turns out to be about 12,800 Km or about the same size as the Earth.
We can also determine the approximate mass of the Sirius dwarf star because we can accurately measure the two stars as they rotate about each other. In a system like the Earth and its Moon where the Earth has six times more mass than the Moon, the Moon mostly rotates around the Earth which does not move very much around the Moon. In the case of Sirius and its white dwarf, they move around each other with the center of gravity approximately halfway between them. This means they have approximately the same mass despite the huge difference in size.
Put another way, the white dwarf has the size of the Earth with a mass about the same as Sirius. This means that the white dwarf star is incredibly dense as we would have predicted knowing it is a white dwarf star. The remaining core has an average density 300,000 times greater than the Earth with 300,000 times the gravity. It is made almost entirely of degenerate matter composed of helium, carbon, and oxygen nuclei filled with a fog of degenerate electrons.
The radius of the white dwarf star is determined by electron degeneracy and is independent of temperature. The matter is tremendously compressed removing much of the empty space between atoms leaving sufficient room for electron orbitals.
No matter how much energy the white dwarf radiates into space, it will remain the same size even as its temperature slowly decreases. The white dwarf star will maintain its size and mass forever, while slowly radiating out heat into space and reducing its temperature.
These facts will help determine the age of the universe.
Electron Degeneracy
Here it might be a good time to say a few more words about electron degeneracy. As we noted, the tremendous gravitational force of a dying star creates extremely high temperatures and pressure at the center of the star. This causes carbon and oxygen to be formed in the core of the white dwarf producing a CO white dwarf star. Most of the white dwarfs are composed of CO combinations at their core.
Sometimes, if the mass of the star is between 8 and 10.5 solar masses, the core temperature of the star will be enough to fuse carbon in which case an oxygen-neon-magnesium white dwarf may form.
The star now reaches a dilemma as the temperature no longer supports fusion into heavier atoms. When the temperature is not enough to produce further fusion, the furnace cools down. The gravitational force then closes in on the core of the white dwarf causing it to contract until the electrons can not be compressed further into unoccupied electron orbits (electron degeneracy).
The star will then gradually cool as it radiates energy; over a very long time period, the white dwarf will cool and its material crystalize. It will gradually not emit significant heat or light and will become a cold black dwarf.
It is thought that there are no black dwarfs in existence because the time required for the white dwarf to cool off is longer than the age of the universe.
White Dwarf Cooling Curves
The essential part of this whole discussion is how the white dwarf will cool over time. They no longer have a nuclear furnace but have converted most of their hydrogen and helium into heavier elements, especially carbon and oxygen. The size of a white dwarf will remain stable even as they gradually cool off over billions of years. The rate at which the white dwarf will cool is dependent upon its luminosity (which depends on its size) and surface temperature.
The white dwarf will cool relatively quickly when it is hot, but the cooler the star becomes, the slower it cools.
We come to know quite a bit about a given white dwarf star. We know the star’s temperature because we know its color, and we know its radius because we know the star’s luminosity. We then can calculate the size volume of the star and because we know the density of degenerate matter in a white dwarf star, then we know the mass. We can then calculate what the luminosity and temperature it will be at any in the future and into the past.
We rarely see very young white dwarf stars because they cool down so quickly; most of the white dwarfs we see are of the intermediate age variety. We know the age of the universe will be older than the oldest white dwarf, but finding old white dwarf stars is tricky because the oldest stars are also dimmest. Therefore, it could be a fair question that if we do not see very old white dwarf stars, it is because they are not there, or because they are too dim for us to see.
The faintest white dwarf stars might have luminosities about 30,000 times less than the Sun with a temperature of about 4,000. The current generation of super-large telescopes has helped to solve this problem. The Sloan Digital Sky Survey provides the most complete data for the observation of white dwarf stars. The survey shows that faint white dwarfs simply are simply not there; the stars in the Milky War (our galaxy) are just too young. The faintest white dwarf stars we can see in our galaxy are on the order of 8.5 to 9.5 billion years old.
Multiple white dwarfs and their cooling curve has been evaluated. We can estimate the rate of cooling of a typical white dwarf star because they have no energy release other than through radiation of its heat. It turns out to be complicated because the rate of cooling varies over time; a cooler star radiates less heat than a hot star would take. Such a model has been developed for a typical carbon white dwarf of 0.59 the sun’s mass. It would take such a star about 1.5 billion years to cool to a surface temperature of 7,140 K; cooling another 500 K would take 0.3 billion years, then next 500 K would take 0.4 billion years, and finally, the next 500 K would take 1.1 billion years.
The oldest white dwarf stars would likely need to be found in our own galaxy as they are too dim to view reliably from further away. One of the most studied stars is only about 28 parsecs from the sun with a surface temperature of 3.780 K with a luminosity that is about 30,000 to 70,000 times fainter than the Sun. It was discovered in 1997 when it was found to have a large proper moving against background stars indicating its close proximity to us. Knowing the star’s distance from its large proper magnitude, the surface temperature from its spectral type, the mass and radius of the star could be calculated and then its rate of cooling estimated. It was thought that the age of this particular cool white dwarf is about 11 billion years. If it is estimated that stars took about 1 to 2 billion years after the big bang to form and a life cycle of about another billion years, the age of the universe can be calculated: Age of star – 11 billion years; the age of the star until white dwarf – 1 billion years; time from big bang until first stars – 1 to 2 billion years; therefore, age of universe about 13-14 billion years.
Summary
White dwarf stars provide another means for the determination of the age of the Universe. The oldest white dwarfs are about 11 – 12 billion years old meaning the Universe is likely about 14 billion years old.
The importance of this determination is to demonstrate the Universe is not infinite in age but has a relatively recent beginning in time. This, along with all the other means for age determination, shows the universe to be about 13.78 billion years old.
References:
Weintraub, David A.; How Old is the Universe? 2011.
related posts
Why Mass Matters
Astronomy found that its mass determines nearly every aspect of a star’s physics; in the end, mass matters most. Its mass and lifespan primarily determine the star’s place on the HR diagram. The star’s position on the HR diagram determines its absolute brightness and color. The problem was that astronomers… Read More »
Why Does the Sun Shine
Astronomers have pondered the question ‘why does the Sun shine” for centuries. Recent discoveries in nuclear physics have finally provided answers to this question. It turns out that the Sun’s radiant energy is explained by our current understanding of nuclear physics. This understanding is explained further below. How Stars Like… Read More »
Stars Are Different
Stars all appear to be about the same; tiny lights in the night sky. However, it may be possible to notice stars of several different colors on a clear night, especially red stars like Antares. Over the last two centuries, much has been learned about differences among the stars and… Read More »
COBE Finds the Big Bang
COBE Finds the Big Bang The COBE satellite was able to find hard evidence for the occurrence of the Big Bang. Further study would make this event one of the best understood and best-documented events in the history of the universe. One of the greatest discoveries of the twentieth century… Read More »