Why Does the Sun Shine
Astronomers have pondered the question ‘why does the Sun shine” for centuries. Recent discoveries in nuclear physics have finally provided answers to this question.
It turns out that the Sun’s radiant energy is explained by our current understanding of nuclear physics. This understanding is explained further below.
How Stars Like the Sun are Formed
The space between stars is mostly very empty with a density about one atom per cubic centimeter.
There are interstellar clouds of matter swirling in space which possess a much greater density. These clouds are in a balance between expansion and collapse.
As the interstellar cloud gradually cools off, expansion loses its fight with gravity and the cloud begins to contract. As the cloud contracts, it will start to rotate faster much like a skater rotates faster with she brings her arms in toward her side.
Angular Momentum
This principle describes the concept of conservation of angular momentum. This principle can be demonstrated with skaters. Drawing a skater’s arms in causes them to spin faster. This same thing happens with interstellar gas formation.
As the gas cloud begins to condense with gravity, it swirls around faster.
There are some areas in this gas cloud that are denser than others, and these denser areas will likely become larger and larger due to their increasing gravitational attraction. Over many millions of years, these dense areas in the gas cloud around stars coalesce into asteroids and planets.
Amazingly, using the Hubble space telescope, it is possible to actually see stars early in their evolutionary growth with gas clouds around them termed a “proplyd”, mimicking the process by which our solar system started.
Sun’s Energy from Gravitational Contraction?
The central portion of this gas cloud will eventually become very dense due to gravitational attraction and become a star.
The way a star shines has only recently been discovered.
Shine from Burning Coal
About two-hundred years ago, the famous German physicist Hermann von Helmholtz calculated that the Sun could not derive its heat from combustible materials like coal or wood because it would only shine for about one-thousand years.
Shine from Gravitational Energy
However, if the Sun were still contracting due to gravity, the conversion of gravitational energy into heat would keep the Sun shining for much longer. Helmholtz calculated this process could cause the Sun to shine for up to 40 million years.
Repeated calculations by the great English physicist Lord Kelvin suggested the conversion of gravitational energy into heat energy could power the Sun for 500 million years. This might provide sufficient time for rocks to form and the Earth to evolve in a natural manner.
The postulate that the Sun’s energy is from gravitation contraction as suggested by Helmholtz and Kelvin could be tested by direct observation.
Testing the Gravitational Energy Hypothesis
The Sun needs to contract by about 70 meters per year in order to produce the heat required. Measuring this small change in the Sun’s circumference was beyond the capability of nineteenth-century science but is well without our twenty-first-century capabilities.
We now know that the Sun is not contracting by this amount, thereby disproving a gravitational source of power.
Why Does the Sun Shine?
The source for the Sun’s energy does not come from gravitational contraction because it is not contracting. The source for the energy to shine for billions of years comes from another source.
The English physicist Arthur Eddington proposed a new method for energy generation in stars based upon Albert Einstein’s theory of special relativity.
One of the tenants of special relativity is that mass is equivalent to energy and that this relationship is correlated with a constant of nature – the speed of light. This formulates the famous equation E = mc2 whereby energy and mass are interrelated by the speed of light; formulated another way, E/m = c2.
Eddington’s Solution
Eddington proposed that four hydrogen nuclei (four protons) could be combined together to make one helium atom. Since the mass of one helium atom is slightly less than the combined masses of four hydrogen atoms, Eddington proposed that this difference represents energy released by this combination.
Astronomer Henry Russell was able to determine in 1929 the relative amounts of elements in the Sun’s atmosphere; he found that more than 90% of the Sun by volume or 45% by mass is composed of hydrogen.
TVisit Sitehe neutron was discovered by James Chadwick and quantum mechanics became a source of intense study during the 1920s and 1930s. Using this knowledge, a physicist named Hans Bethe deduced the sequence of nuclear reactions that takes place in the cores of stars to allow them to shine.
The Proton-Proton Chain
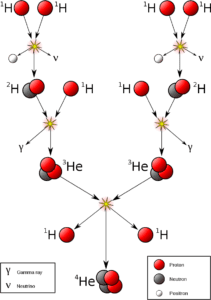
Proton-Proton Reaction
- In a series of reactions, four protons (hydrogen nucleus) combine to form a single helium nucleus made of two protons and two neutrons. It would be highly unlikely for four hydrogen atoms to collide at precisely the same moment for this fusion to occur in one step. Instead, there is a chain of intermediate events to bring about the production of helium using a much more likely series of events.
- First, two protons collide
- After this collision, one of the protons is converted into a neutron through the emission of a positron (the antiparticle equivalent of an electron) and a neutrino. The resulting particle with a proton and a neutron is an isotope of hydrogen called deuterium.
- The positron will in short order hit its anti-particle (an electron) and in this collision, they will destroy each other producing energy in the form of a gamma-ray photon. This high-energy photon then strikes other particles causing them to move more quickly increasing the Sun’s heat. The neutrino only very rarely interacts with other matter and flies right out of the Sun.
- The deuterium nucleus then collides with a proton to form an isotope of helium with two protons and one neutron (normal helium has two neutrons). This reaction also produces energy in the form of a gamma-ray which will also interact with other atoms increasing their energy and thereby increasing heat in the center of the Sun.
- Two helium isotopes then collide with each other forming a normal helium atom (with two protons and two neutrons) along with two protons. The combined mass of four protons is 6.690 X 10-24 grams while the mass of one helium nucleus is 6.643 X 10-24 grams; the difference is equal to 0.7% of the starting mass which represents the mass converted to energy.
If the entire mass of the Sun were available for the proton-proton chain reaction (which it is not), then the Sun could shine for 100 billion years.
The Sun’s Fusion Energy
The proton-proton reaction is the stuff dreams are made from. Mankind is now urgently trying to make fusion power possible as it would provide almost limitless power with no toxic waste (such as with conventional nuclear power plants which work by fission – not fusion).
The problem is with the first step of the reaction; two protons do not want to collide and stick together. The two protons are positively charged, so the electromagnetic force will cause them to repel each other. For the two protons to stick, they must collide at tremendous energy to come closer than one nuclear diameter (10^-13cm). The minimum energy to overcome their mutual repulsion is 10 billion degrees K.
This poses a problem because the star interiors are not nearly 10 billion degrees; they are actually about 10 million degrees hot.
Solving the Inadequate Heat Dilemma
Quantum physics provides the way out of the inadequate hear dilemma.
- The Sun’s average core temperature is about 10 million degrees; however, not every area within this core has the same temperature. There is a distribution of temperatures with some areas being cooler and some being much hotter. There is a mathematical expression of this difference called the Maxwell-Boltzmann distribution. According to this distribution, there will be a few protons with a temperature of 10 billion degrees if the average temperature is only 10 million degrees.
- There is a process called “quantum tunneling” which also comes into play when considering nuclear reactions within the Sun.
Quantum Tunneling
Quantum tunneling was first proposed by the Russian physicist George Gamow in 1928. The basic idea is that in the quantum (or subatomic) world of physics, unlikely things may happen frequently.
Two protons normally could not approach each other close enough with temperatures in the Sun’s core, even when allowing for regionally higher temperatures predicted by the Maxwell-Boltzmann distribution noted above; their mutual repulsion is just too strong.
Quantum tunneling suggests that even though very unlikely, two protons might get close enough once in 10 billion years. However, because the sun has tremendous amounts of protons (about 10^55), enough of these unlikely collisions happen every second (about 10^38 per second) that the sun is able to shine.
The Sun converts about 600 million tons of hydrogen to 596 million tons of helium; the difference (4 tons) is the amount of hydrogen which is converted into energy.
When the Sun Ages
Eventually, much of the hydrogen in the Sun’s core will be converted into helium, the nuclear reaction will slow down, and the core will cool.
When the Sun cools, it will contract slightly due to gravitational forces achieving the advantage of heat expansion. When the Sun contracts, temperatures will increase more and lead to a new set of nuclear reactions. These internal structural changes will cause the Sun to increase in size until it becomes a red giant star.
The Sun can convert about 0.7% of its mass into helium nuclei before it runs into trouble. It is calculated that this will take about 10 billion years to accomplish. Since our Sun is nearly five years old, it is now firmly in middle age.
How Old is the Sun?
The rate of nuclear reactions at the Sun’s core depends upon the Sun’s core density, temperature, and pressure. As helium accumulates, the process of hydrogen conversion into helium becomes slightly less efficient. This will cause the Sun to contract increasing its temperature and luminosity.
Given the mass and composition of the Sun, physicists can calculate the luminosity and temperature of the Sun over time. They know its luminosity when it was born. They can also calculate how it varies over time. From these calculations, the age of the Sun is calculated to be about 4.5 billion years old.
The Sun is about the same age as the oldest meteorites. It is also only slightly older than the oldest rocks on Earth (about 4.1 billion years).
Why This is Important
There are now two independent means for establishing the minimum age of the Universe: radioactive decay and rate of thermonuclear reactions in the Sun. The logical nature of these calculations lends some credence that they are correct.
The Sun, asteroids, and earth are all approximately the same age.
Summary
There was very significant growth in our knowledge of astrophysics during the last century. Scientists are now able to answer the question, “why does the Sun shine?”
We also know that the Sun will shine for billions of years without running out of fuel.
Scientists n the nineteenth century thought the Sun was burning coal. This would not produce nearly enough energy and would have burned out by now.
Alternatively, some had thought that gravitational energy could be converted into heat energy and that keeps the Sun burning. However, the Sun has not contracted nearly enough to produce that amount of energy.
The Sun’s radiation energy can generate ts emitted energy over billions of years.
It is almost certainly correct.
related posts
Why Mass Matters
Astronomy found that its mass determines nearly every aspect of a star’s physics; in the end, mass matters most. Its mass and lifespan primarily determine the star’s place on the HR diagram. The star’s position on the HR diagram determines its absolute brightness and color. The problem was that astronomers… Read More »
White Dwarf Stars
The age of white dwarf stars is one of the best ways to help determine the age of the universe. We took a brief look at how this is done. But to really understand how this is done, it is necessary to take a deep dive into what a white… Read More »
Big Bang Confirmed
The existence of the Big Bang has been confirmed through multiple independent mechanisms to have occurred about 13.78 billion years ago. We can even measure the left-over temperature from the Big Bang in empty space. Two of the greatest discoveries made in cosmology during the twentieth century were that the… Read More »
COBE Finds the Big Bang
COBE Finds the Big Bang The COBE satellite was able to find hard evidence for the occurrence of the Big Bang. Further study would make this event one of the best understood and best-documented events in the history of the universe. One of the greatest discoveries of the twentieth century… Read More »